In a groundbreaking study published by researchers from Freie Universität Berlin, University of Maryland, NIST, Google AI, and Abu Dhabi, significant strides have been made in the field of quantum simulation, particularly regarding the estimation of Hamiltonian parameters associated with bosonic excitations. This development, documented in their pre-published paper on arXiv, is poised to enhance the precision of quantum simulations beyond what classical computers can achieve. The collective efforts of these researchers highlight a crucial intersection of theory and application, showcasing the potential for new methodologies to reshape our understanding of quantum systems.
The train of innovation within this research journey began during a conference in Brazil when Jens Eisert, the first author, received a call from colleagues in the Google AI team. They were struggling to calibrate their Sycamore superconducting quantum chip using Hamiltonian learning techniques. Initially, Eisert believed the problem could be solved quickly, but as they delved deeper, it became clear that accurately recovering the frequencies of the Hamiltonian operator presented a daunting challenge. This situation prompted the collaboration with two bright Ph.D. students, Ingo Roth and Dominik Hangleiter, who joined forces to find a viable solution.
Despite an initial sense of optimism, the trio discovered that their theoretical ideas needed refinement to withstand the rigors of large-scale experiments. After a prolonged struggle, compounded by the complexities of the Hamiltonian dynamics, their perseverance bore fruit, culminating in the successful application of their innovative Hamiltonian learning techniques.
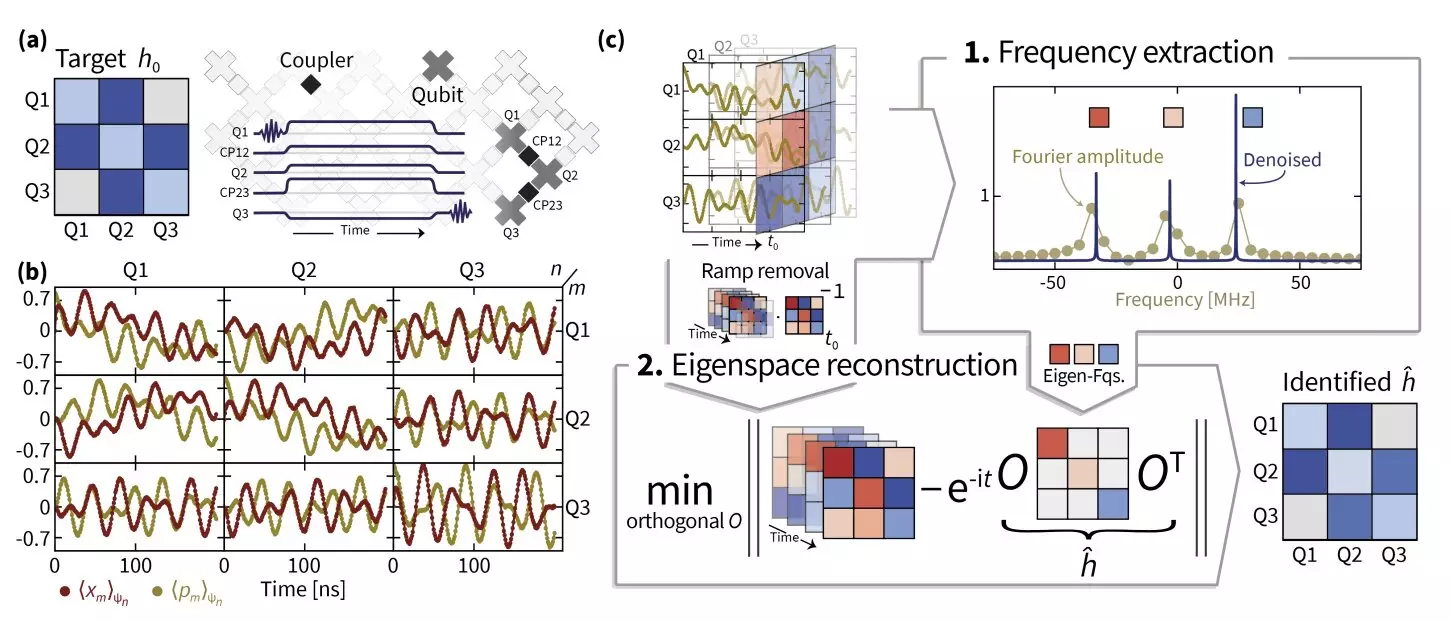
The research team employed several advanced methodologies to grasp the Hamiltonian dynamics of their superconducting quantum simulator. Central to their approach was the adoption of superresolution techniques, allowing for enhanced resolution in estimating eigenvalues and thus uncovering the correct frequencies of the Hamiltonian. Complementing this was a technique known as manifold optimization, which involves specialized algorithms designed for tackling complex optimization problems within non-linear, curved spaces—essentially navigating the particular challenges posed by the manifold structure of quantum Hamiltonians.
Eisert and his collaborators recognized that effective learning of Hamiltonians relies heavily on the precise understanding of switch-on and switch-off dynamics, as these processes are inherently imperfect and non-instantaneous. Their innovative signal processing methods, dubbed TensorEsprit, played a pivotal role in enabling robust estimations even for larger quantum systems. This integration of methodologies reflects the intricate nature of quantum simulator dynamics, with the team acknowledging the difficulty of translating theoretical frameworks into practical implementations with actual quantum data.
The implications of this research extend far beyond theoretical considerations. The methods developed by the team, particularly their enhancements in Hamiltonian learning, indicate a strong potential for scalability and robustness within large quantum processors. As these techniques mature, they may serve as a cornerstone for future developments aimed at identifying Hamiltonian parameters across a variety of quantum systems, fostering a richer understanding of quantum mechanics.
Looking ahead, Eisert and his team plan to apply their methods to interacting quantum systems and explore tensor network-inspired approaches, particularly within systems involving cold atoms, as initially introduced by physicist Immanuel Bloch. This direction underscores the long-term vision of enhancing the capabilities of quantum research and technologies by tackling fundamental questions about the nature of Hamiltonians.
A critical dimension of this research pertains to the very essence of the Hamiltonian operator and its implications for predictive capabilities in quantum mechanics. The researchers emphasize that while the Hamiltonian characterizes the system, it is often presumed to be known, which can be misleading. The task of discerning the Hamiltonian from experimental data becomes vital because predictive power in quantum mechanics hinges on an accurate understanding of the Hamiltonian.
Eisert’s insights into the future significance of Hamiltonian learning resonate with the broader scientific community’s endeavors to leverage analog quantum simulation techniques. By creating highly controlled experimental conditions mimicking complex quantum systems and materials, these advancements promise to lead to unprecedented precision in quantum simulations.
The fusion of innovative methodologies in Hamiltonian learning and a comprehensive understanding of quantum dynamics not only enriches theoretical discourse but also paves the way for significant advancements in quantum technology, potentially unlocking new realms of research in both the fundamental and applied sciences of quantum mechanics.

Leave a Reply
You must be logged in to post a comment.