The Importance of Logarithmic Step Size in Stochastic Gradient Descent Optimization

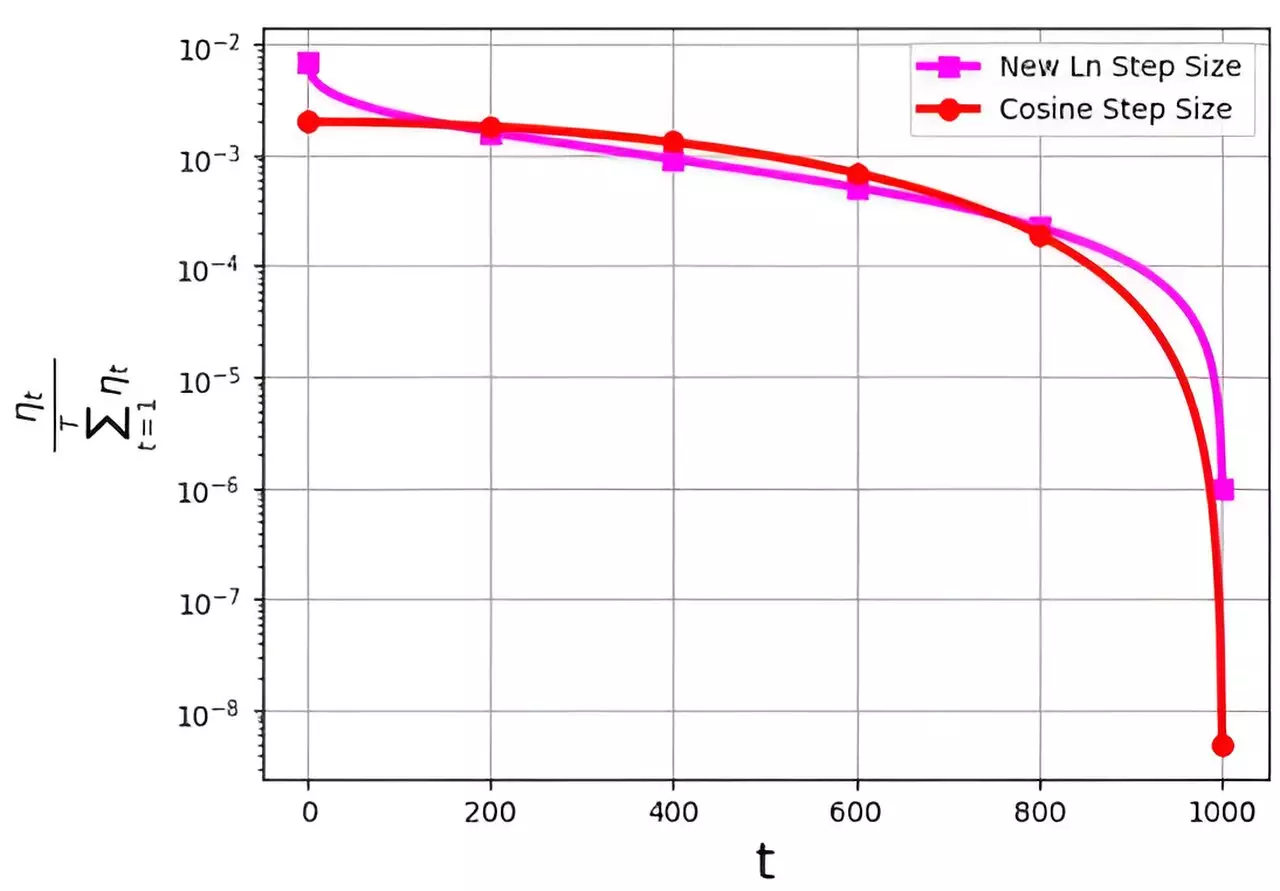
In the realm of optimizing the stochastic gradient descent (SGD) algorithm, the step size, commonly known as the learning rate, plays a crucial role. Various strategies have been devised to improve the performance of SGD, with a key challenge revolving around the probability distribution of the step sizes assigned to iterations. The distribution ηt/ΣTt=1ηt tends to avoid assigning extremely small values to final iterations, a drawback observed in the popular cosine step size method.

Research on Logarithmic Step Size

A recent study led by M. Soheil Shamaee, detailed in Frontiers of Computer Science, introduces a novel approach to step size in SGD. The logarithmic step size method addresses the issue faced by the cosine step size, particularly in the final iterations. By providing a significantly higher probability of selection during crucial concluding phases, the logarithmic step size outperforms the cosine method. This improvement is evidenced by numerical results obtained from experiments conducted on datasets such as FashionMinst, CIFAR10, and CIFAR100.

Impact on Performance

The effectiveness of the new logarithmic step size is further highlighted by its impact on test accuracy. When applied in conjunction with a convolutional neural network (CNN) model on the CIFAR100 dataset, the logarithmic method results in a notable 0.9% increase in accuracy. This underscores the importance of choosing an appropriate step size strategy in SGD optimization to achieve enhanced performance outcomes.

The introduction of the logarithmic step size for the SGD algorithm represents a significant advancement in optimizing efficiency. By addressing the limitations of existing step size methods, such as the cosine approach, the logarithmic strategy demonstrates superior performance in critical iterations. The research findings underscore the importance of continuous innovation in step size strategies to further enhance the capabilities of SGD in machine learning applications.